Introduction au Deep Learning

Nous pouvons imaginer un algorithme capable, à partir d’une image, de nous dire précisément ce dont il s’agit. Par exemple, à partir d’une photographie de vache notre algorithme doit être en mesure de nous dire qu’il s’agit bien d’une vache.
Pour faire en sorte que notre machine apprenne, nous allons l’entraîner sur un ensemble important d’images dont on connait la réponse. C’est ce qu’on appelle un ensemble d’apprentissage. Dans cette base d’apprentissage, on peut trouver des images et leurs étiquettes, comme présenté dans l’exemple suivant :
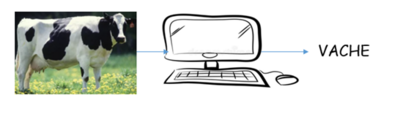
Ce processus s’appelle « apprentissage supervisé » ou « supervised learning » en anglais. A chaque fois, on donne une image à notre machine afin de lui faire apprendre son étiquette réelle (VACHE / PAS VACHE) :
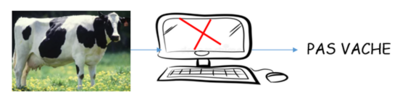
Et si jamais notre machine se trompe :
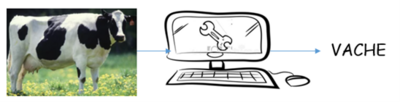
Au cours du processus d’apprentissage, on va lui dire, : « ta réponse est incorrecte, ajuste-toi pour nous prédire la bonne réponse ». La machine va devoir procéder à un certain nombre de réglages pour apprendre à nous donner le résultat qu’on espère avoir.
Une fois la phase d’entrainement est achevée, notre machine est censée être capable de nous dire s’il s’agit bien d’une photographie de vache ou non avec une certaine précision que nous espérons la plus robuste possible.
Mais qu'est-ce qui se cache sous le capot de cette machine ?
Comme beaucoup de choses dans la vie courante, les ingénieurs se sont inspirés de la vie réelle et plus particulièrement du fonctionnement du cerveau car il est à l’origine de l’apprentissage chez les êtres vivants. A l’intérieur d’un cerveau se trouvent des milliards de neurones qui se transmettent de l’information.
Il est manifeste qu’un cerveau est extrêmement complexe. Les ingénieurs ne peuvent pas programmer un cerveau tel qu’il existe chez les êtres vivants. D’ailleurs les meilleurs scientifiques du monde ont encore des difficultés à comprendre comment fonctionne l’ensemble du cerveau. Les ingénieurs ont donc programmé une abstraction de celui-ci. La figure suivante montre un cerveau (en rouge) avec plusieurs connexions complexes. Le réseau de neurones (en bleu), superposé sur la même figure, ne représente qu’une conceptualisation très modeste du fonctionnement d’un cerveau.
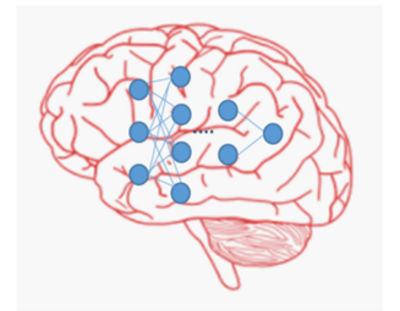
Pour comprendre le fonctionnement d’un réseau de neurones qui est la base du Deep-Learning, nous allons prendre un petit réseau constitué de six neurones, connectés via des câbles, qui appartiennent à des familles différentes : famille des entrées (inputs), famille des couches cachées (hidden layers) et famille des sorties (outputs).
Dans l’exemple suivant, nous avons deux neurones appartenant à la couche d’entrée. Les trois neurones suivants appartiennent à la couche cachée et un neurone appartenant à la couche de sortie :
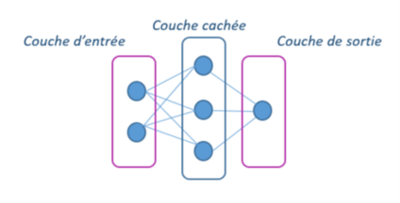
Ce réseau de neurones est très simple, mais on peut avoir un réseau de neurones avec autant de neurones qu’on veut par famille. On peut avoir également plusieurs couches cachées. C’est d’ailleurs de là que vient l’appellation Deep-Learning qui signifie apprentissage profond en anglais. Tout ce qu’on va voir ici avec ce simple réseau s’applique également sur les réseaux de neurones complexes.
Feed forward
Une étape clé pour comprendre comment fonctionnent les réseaux de neurones, c’est la phase du Feed forward. On donne des valeurs à nos neurones en entrée qu’on combine, via des câbles, pour transmettre cette information vers la couche cachée. Ensuite de la couche cachée vers la couche de sortie.
Regardons en détails comment ces valeurs sont transmises d’un neurone vers un autre. Pour cela, prenons un exemple encore plus simple, deux neurones qui se connectent à un seul neurone dans la couche suivante :
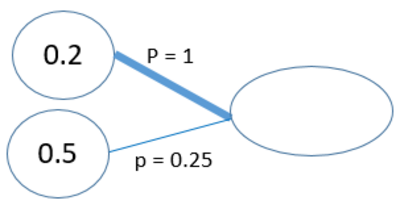
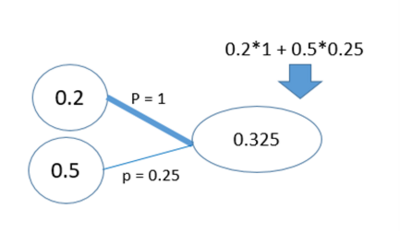
Le premier neurone vaut 0.2 et le deuxième vaut 0.5. On épaissit un câble comme si on pouvait passer plusieurs choses via celui-ci. L’épaisseur de notre câble est représentée par une valeur, c’est ce qu’on appelle le poids de la connexion. Afin de transmettre l’information de l’entrée vers le neurone de la couche suivante, on multiplie les entrées par leurs poids de connexion : 0.2 x 1 et 0.5 x 0.25. On additionne ensuite les résultats de ces deux multiplications, on obtient la valeur de 0.325, comme le montre la figure suivante :
Le dernier neurone récupère la valeur 0.325 comme son entrée, mais avant de la transmettre au neurone de la couche suivante il va devoir la modifier à l’aide d’une fonction mathématique. Cette fonction s’appelle la fonction d’activation f. Elle est là pour déterminer quelle valeur on doit passer au neurone suivant :
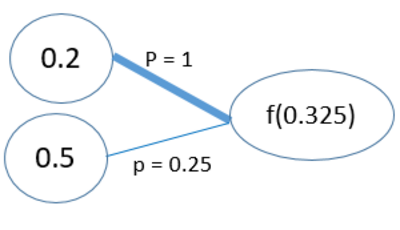
Etape 1 - produit scalaire
Le résultat de cette fonction peut aussi se rapprocher de 0. On dit alors que le neurone ne s’active pas, d’où l’analogie avec ce que l’on retrouve dans notre cerveau. En effet, il y a des neurones qui s’activent et d’autres qui sont en pause.
Si on récapitule, nous avons un ensemble de neurones dans notre réseau connectés entre eux. On rentre nos données dans la couche d’entrée. Ces neurones sont connectés aux neurones suivants à l’aide des câbles. L’épaisseur de ces câbles est caractérisée par des poids. Plus le poids est important, plus le câble est épais, plus l’information transmise dans la connexion est importante.
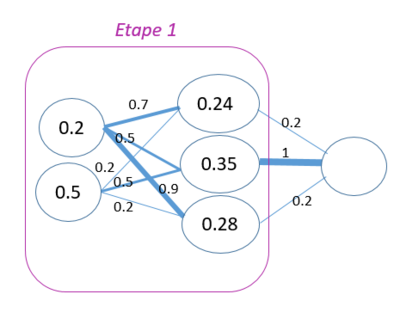
Nous pouvons prendre à titre d’exemple le réseau présenté dans la figure 6 alimenté par des données dans la couche d’entrée [0.2, 0.5] ainsi que les poids reliant la couche d’entrée à la couche cachée.
Dans l’étape 1 du calcul, chaque neurone de la couche cachée reçoit l’information transmise par la couche d’entrée pondérée par les poids de leur connexion. Ainsi, la valeur 0.24 obtenue pour le premier neurone est le résultat de la multiplication des valeurs en entrée par leurs poids de connexion au neurone de la couche cachée, suivi d’une sommation : 0.2 x 0.7 + 0.5 x 0.2 = 0.24
Etape 2 – fonction d’activation
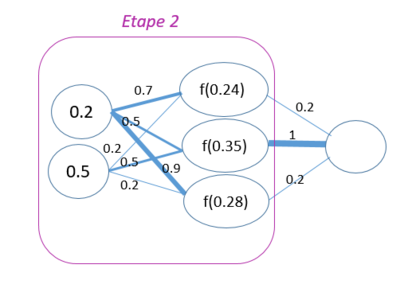
Dans l’étape 2 de l’algorithme, les résultats reçus dans la couche cachée passent dans la fonction d’activation.
Ici, nous allons utiliser la fonction d’activation logistique : f(x)=1/ (1+exp (-x))
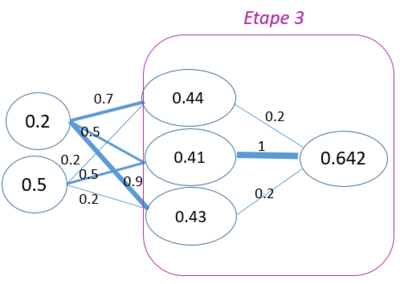
Dans l’étape 3 de la phase feed forward, l’information reçue dans la couche cachée est transmise vers la couche de sortie en suivant les mêmes calculs que ceux présentés précédemment.
La prédiction de notre réseau en fonction des valeurs qu’on lui a donné en entrée est de 0.642. Il y a assez peu de chance que cette réponse soit bonne, puisque notre réseau n’a pas encore été entraîné : au départ, les valeurs des poids affichées dans notre réseau ont été choisies de manière arbitraire et donc la réponse a très peu de chance d’être correcte.
Imaginons que les valeurs en entrée de notre réseau [0.2, 0.5] ont une valeur observée de [0.7] comme output dans notre ensemble d’apprentissage. La prédiction donnée par notre réseau est de 0.642. Grâce à ces deux valeurs (observée et prédite), nous allons pouvoir calculer à quel point notre réseau s’est trompé. C’est ce qu’on appelle la fonction d’erreur. Il existe plusieurs fonctions d’erreur dans la littérature. Nous nous contentons de la fonction d’erreur suivante : ½ (o-p)². Il s’agit d’une opération qui va calculer la différence entre ce qu’on a observé et ce qu’on a prédit. Le carré de la différence est rajouté pour avoir une valeur positive. Le facteur ½ et rajouté pour faciliter d’autres étapes de calcul. Si on remplace o et p par leurs valeurs dans la formule, on obtient comme résultat de la fonction d’erreur 0.002 :
½ (o-p)2= ½ (0.7-0.642)2 = 0.002
Si l’erreur avait été très proche 0, on aurait supposé qu’il n’y a pas d’erreur et que le réseau a correctement répondu. Comme ce n’est pas le cas, on essaie de modifier les poids du réseau pour pouvoir la faire baisser. Mais comment modifier les poids du réseau ? Pour répondre à cette question on va s’intéresser à la prochaine étape appelé la rétro-propagation (back propagation).
Rétro-propagation
L’explication de cette étape de rétro-propagation d’erreur nécessite qu’on rentre dans des détails mathématiques un peu plus complexes. Dans cette partie nous allons présenter le concept autour de la rétro-propagation sans renter dans des considérations mathématiques.
Prenons à titre d’exemple le cas d’un enfant que l’on grognonne pour lui faire comprendre que son comportement n’est pas approprié. La rétro-propagation est le fait de transmettre à son cerveau l’apprentissage suivant : « Il ne faut plus dessiner sur un mur ».
Dans la phase d’apprentissage on va vérifier si la sortie de notre réseau est correcte vis-à-vis de la sortie observée dans l’ensemble d’apprentissage. Si ce n’est pas le cas, on va procéder par une rétro-propagation d’erreur visant à modifier les poids de notre réseau, assignant ainsi des responsabilités partagées de l’erreur aux différentes connexions.
Revenons à notre réseau de neurones présenté précédemment. Nous allons faire un petit essai en changeant le poids affichés en orange, comme le montre la figure suivante :
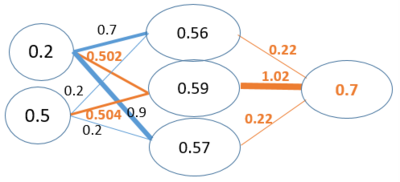
Cette opération a permis de donner une estimation plus précise 0.7 en la comparant avec celle obtenue au précédemment (0.642). Rappelons que la donnée observée comme output dans notre ensemble d’apprentissage est de 0.7. En faisant cette opération, nous avons réussi à donner une estimation plus précise. Ce qui veut dire que les connexions ajustées par l’algorithme ont un impact significatif sur l’erreur.
Si on répète ce processus sur l’ensemble des poids de notre réseau, avec plusieurs exemples de l’ensemble d’apprentissage, on va donc équilibrer tous les poids de notre réseau et ainsi minimiser l’erreur globale. Cette phase d’apprentissage va nous permettre de trouver la meilleure combinaison de poids qui donnera des estimations les plus proches possibles de nos outputs observés. Par conséquent, lorsqu’on donnera à notre réseau, bien entraîné, des valeurs inconnues ne faisant pas partie de l’ensemble d’apprentissage, il devrait nous donner une prédiction en adéquation avec le résultat attendu.
Bibliographie
[1] Larose D.T. 2005. Des données à la connaissance, Vuibert Informatique
[2] Les réseaux de neurones pour les nuls
[3] Comprendre le deep learning et les Résaux de neurones en 10 mins !
